ELEKTRONIKA DAN SISTEM DIGITAL: TUGAS BESAR PENGENALAN OPTIMASI NEW EDITION

Referensi :

Nurhayati, A. Jaya, Nawal. Aliyansyah, Achmad Nur. Pagiling, Luther., (2022). "Analisis Tunning Parameter PID Menggunakan Algoritma Genetika pada Pengontrolan Kecepatan Motor DC". Jurnal Majalah Ilmiah Teknologi Elektro Vol. 21, No. 2, Juli - Desember 2022.

DAFTAR ISI

1. Judul

2. Abstrak

3. Pendahuluan

4. Tinjauan Pustaka

5. Hasil dan Pembahasan

Analisis Tuning Parameter PID Menggunakan Algoritma Genetika pada Pengontrolan Kecepatan Motor DC

Abstrak[Kembali]

Pengaplikasian motor DC sering mengalami ketidakstabilan kecepatan putaran akibat adanya pembebanan saat dioperasikan. Untuk mengatasinya kontrol PID dapat diaplikasikan untuk menstabilkan kecepatan. Kontrol PID merupakan kombinasi dari pengendalian proportional, integral dan derivative. Untuk mendapatkan performa yang baik diperlukan penalaan (tuning) ketiga parameter ini menggunakan beberapa metode, salah satunya algoritma genetika. Algoritma genetika bekerja dengan membentuk populasi dari beberapa individu yang berpotensi menghasilkan solusi optimal dinilai dari nilai ketahanannya (fitness). Beberapa parameter digunakan dalam algoritma genetika seperti ukuran populasi, jumlah generasi, probabilitas crossover dan probabilitas mutasi. Penelitian ini bertujuan untuk menganalisis metode algoritma genetika untuk tuning parameter kontrol PID pada pengontrolan kecepatan putaran motor DC. Hasil pengujian diperoleh parameter algoritma genetika dengan ukuran populasi dan jumlah generasi sebesar 70, probabilitas crossover sebesar 0,9 dan probabilitas mutasi sebesar 0,4 dengan nilai fitness sebesar 6,261e+18. Parameter kontrol PID dengan nilai Kp = 9,4429; Ki = 19,3255 dan Kd = 0,45602 dan respon sistem dengan nilai rise time sebesar 0,1212 s, settling time sebesar 0,2562 s, overshoot sebesar 0,0366 % dan steady-state error sebesar 0,1739 %. Dengan parameter kontrol PID ini motor DC mampu bekerja mengikuti setpoint baik pada keadaan nilai beban yang tetap maupun berubah.

Pendahuluan[Kembali]

Motor DC merupakan perangkat elektromagnetis yang saat ini skala penggunaannya sangat luas, mencakup bidang industri, robotika, hingga peralatan rumah tangga [1]. Hal ini tidak lepas dari keunggulan motor DC seperti memiliki pengoperasian yang mudah, torsi awal yang tinggi, serta sistem pengontrolan yang lebih sederhana dan ekonomis [2]. Namun dalam pengoperasiannya, kecepatan putaran pada motor DC dapat mengalami penurunan akibat pembebanan. Untuk mengatasinya dapat dilakukan dengan mengatur masukan tegangan untuk menjaga kestabilan kecepatan putaran [3]. Maka dari itu diperlukan sistem pengendali yang mampu mempertahankan kinerja motor DC agar tetap stabil.

Sistem pengendalian sangat penting guna mengoptimalkan kinerja atau performa sebuah sistem, mengurangi human error serta mengefisiensikan waktu pengoperasian [4]. Pengendali PID digunakan secara luas dalam kontrol proses. Sekitar 95% operasi closed-loop pada bidang otomasi menggunakan pengontrol PID [5]. Kontrol PID merupakan pilihan yang paling baik karena memiliki struktur yang simpel, efisiensi yang tinggi serta mudah dalam pengaplikasiannya. Kontrol PID merupakan kombinasi dari tiga parameter pengendalian yaitu proportional, integral dan derivative [6]. Kontrol PID bekerja menggunakan mekanisme umpan balik untuk mengoreksi penyimpangan nilai aktualnya terhadap setpoint [7]. Untuk mendapatkan performa yang diinginkan diperlukan penalaan (tuning) ketiga parameter pengendalian ini. Terdapat beberapa metode tuning parameter PID seperti trial and error, Ziegler Nichols, Coefficient Diagram Method (CDM), Fuzzy Tuning, Neural Network dan Intelligent Search Algorithm. Namun, beberapa metode tersebut masih memiliki kelemahan seperti trial and error yang kurang efektif dan tidak memiliki prosedur standar, Ziegler Nichols yang masih menghasilkan overshoot tinggi, atau metode Fuzzy yang rumit untuk didesain terutama untuk sistem yang tidak memiliki data eksperimen terdahulu [8].

Intelligent search algorithm merupakan metode tuning lainnya yang bekerja dengan melakukan iterasi berulang untuk mendapatkan nilai parameter terbaik. Kelebihan metode ini yaitu mampu menyelesaikan permasalahan yang kompleks [8]. Algoritma genetika sebagai salah satunya telah banyak digunakan dalam optimasi permasalahan termasuk dalam sistem pengontrolan. Algoritma ini bekerja dengan membentuk populasi dari beberapa solusi yang potensial dinilai dari nilai ketahanan (fitness) masing-masing individu [9]. Algoritma genetika mampu menyelesaikan persoalan yang tidak dapat diselesaikan dengan perhitungan matematika biasa dan memberikan hasil yang baik untuk permasalahan optimasi [10]. Teknik pencarian ini meniru proses evolusi dimana sekumpulan calon solusi yang memiliki nilai ketahanan terbaik akan bereproduksi dan bermutasi untuk menghasilkan generasi selanjutnya. Proses ini akan terus berlanjut dimana tiap individu pada tiap generasi akan dilakukan evaluasi ketahanannya hingga diperoleh hasil yang paling optimal untuk sistem [11].

Penelitian terhadap proses tuning PID dengan algoritma genetika yang telah dilakukan menunjukkan respon sistem yang stabil dan mampu meredam gangguan [12]. Penelitian lain juga dilakukan dalam bentuk simulasi terhadap pengontrolan motor DC [13], [14] maupun impelementasinya secara langsung [15] menunjukkan respon sistem yang baik. Pada proses pengontrolan PID dengan algoritma genetika ada beberapa parameter yang harus ditentukan seperti ukuran populasi, probabilitas crossover, probabilitas mutasi, probabilitas seleksi, jumlah generasi, metode seleksi dan fungsi fitness [9]. Pemilihan parameter ini dapat memberi pengaruh yang signifikan pada performa algoritma genetika untuk menentukan parameter kontrol PID. Selain parameter tersebut pemilihan fungsi fitness juga sangat mempengaruhi hasil yang diperoleh. Pada penelitian [16] Inverse Integral Squared Error digunakan sebagai fungsi fitness untuk metode African Buffalo Optimization-PID (ABO-PID) pada Automatic Voltage Regulator (AVR) menunjukkan respon sistem yang baik. Maka dari itu pada penelitian ini dilakukan simulasi kontrol PID dengan metode algoritma genetika dengan fungsi fitness berupa Inverse Integral Squared Error untuk menganalisa performa sistem yang dihasilkan dalam pengontrolan kecepatan motor DC.

Tinjauan Pustaka[Kembali]

A. Motor DC

Motor DC merupakan mesin yang menggunakan energi listrik arus searah untuk menghasilkan energi mekanis. Prinsip kerja motor DC yaitu ketika sebuah kumparan yang dialiri arus listrik ditempatkan pada medan magnet maka akan terbentuk gerak putar atau gaya pada kumparan tersebut [17]. Pemodelan sistem motor DC ditunjukkan dalam rangkaian ekivalen pada gambar 1.

Pemodelan motor DC dapat diperoleh dengan analisa secara elektrikal dan secara mekanikal. Secara elektrikal didasarkan pada Hukum Tegangan Kirchhoff (KVL) [8] Persamaannya sebagai berikut

Keterangan :

V = tegangan jangkar (V) Vemf = tegangan balik motor (V) L = induktansi jangkar (H)

R = tahanan jangkar (Ω)

T = torsi motor (Nm)

J = momen inersia motor (kgm2)

ω = kecepatan putaran motor (rad/s)

Kt	=	konstanta torsi (Nm/A)
Kb	=	konstanta gaya gesek (Nm/rad/s)
Ke	=	konstanta tegangan balik (V/rad/s)

B. Sistem Kontrol

Sistem kontrol merupakan sistem yang mengintegrasikan proses yang akan dikontrol (plant), aktuator, sensor dan kontroler untuk mempertahankan keluaran dan unjuk kerja sistem tetap pada nilai yang ditentukan (setpoint) [18].

C. Performa Sistem Kontrol

Sebuah sistem memiliki karakteristik atau ciri khusus yang menggambarkan perilaku dinamik sistem atau yang dikenal juga dengan spesifikasi performa sistem. Respon keluaran muncul ketika sistem diberikan suatu sinyal masukan atau sinyal uji [19]. Untuk mengukur performa sistem kendali, biasanya digunakan beberapa parameter yang diperoleh dari respon transien sistem yaitu karakteristik nilai waktu tunda (delay time), waktu naik (rise time), waktu puncak (peak time), maksimum overshoot, waktu tunak (settling time), dan steady- state error [20].

D. Kontrol PID

Kontroler PID merupakan kontroler yang menggunakan mekanisme umpan balik untuk menetapkan presisi atau ketelitian suatu sistem instrumentasi. Komponen kontrol PID memiliki tiga jenis yaitu kontrol proportional, kontrol integral dan kontrol derivative. Ketiga parameter kontrol ini sangat mempengaruhi karakteristik kontroler PID [21], [22].

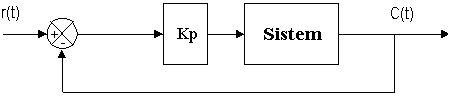
1) Kontrol Proportional (P): Kontrol proportional adalah pengendali yang menghasilkan output dengan mengalikan konstanta proportional gain (Kp) dengan nilai error.

2) Kontrol Integral (I): Kontrol integral merupakan pengendali yang bekerja dengan mengakumulasi error yang terjadi dalam rentang waktu tertentu kemudian mengalikannya dengan sebuah konstanta integaral gain (Ki).

3) Kontrol Derivative (D): Kontrol derivative (D) merupakan pengendali yang memberikan aksi pengendalian dengan mengalikan konstanta derivative gain (Kd) dengan laju perubahan sinyal error.

Kombinasi Kontrol Proportional, Integral dan Derivative: Ketiga jenis kontrol PID dapat digabungkan untuk mendapatkan respon output yang lebih baik. Perubahan pada salah satu konstanta dapat mempengaruhi keseluruhan respon sistem. Pengaruh dari masing-masing konstanta PID dirincikan pada tabel 1 [20].

Berdasarakan tabel 1 diketahui bahwa konstanta P bersifat menurunkan nilai rise time dan steady-state error, mengubah sedikit nilai settling time dan meningkatkan overshoot. Konstanta I bersifat menurunkan nilai rise time, meningkatkan nilai settling time dan overshoot serta menghilangkan steady- state error. Sedangkan konstanta D bersifat mengubah sedikit nilai rise time dan stedy-state error serta menurunkan nilai settling time dan overshoot. Besarnya keluaran dari kontrol PID merupakan akumulasi dari ketiga pengontrolannya sehingga dapat dirumuskan dengan persamaan berikut.

E. Algoritma Genetika

Algoritma genetika merupakan suatu teknik optimasi dan teknik pencarian yang diadopsi dari proses evolusi alam dan perubahan pada struktur genetika makhluk hidup. John Holland menemukan bahwa algoritma genetika mampu menyelesaikan persoalan yang tidak dapat diselesaikan dengan perhitungan matematika biasa dan memberikan hasil yang baik untuk permasalahan optimasi [10]. Algoritma genetika berjalan dengan siklus yang diilustrasikan pada gambar 2.

Berdasarkan gambar 2 dapat diuraikan siklus algoritma genetika yang dimulai dengan inisialisasi populasi yaitu pembentukan populasi secara acak yang terdiri atas beberapa individu yang disebut kromosom dimana tiap kromosom merepresentasikan calon solusi yang memiliki potensi untuk penyelesaian masalah. Pada tiap siklus populasi ini akan melalui tahap evaluasi berdasarkan nilai fitnessnya, dimana kromosom yang memiliki nilai fitness terbaik memiliki peluang besar untuk bertahan pada generasi selanjutnya. Tahap berikutnya yaitu seleksi untuk memilih kromosom-kromosom yang dijadikan sebagai orang tua (parents) untuk membentuk kromosom baru. Pada tahap reproduksi kromosom-kromosom yang terpilih sebagai parents akan melalui dua operator algoritma genetika, yaitu penyilangan (crossover) dan mutasi (mutation) yang akan mengubah struktur gen kromosom begitu pula nilai fitnessnya. Terakhir yaitu tahap pembentukan populasi baru dimana kromosom-kromosom baru yang terbentuk kemudian akan menggantikan kromosom-kromosom dalam populasi dari generasi sebelumnya. Untuk mencegah terjadinya penurunan nilai fitness selama tahap reproduksi kromosom dilakukan prosedur elitisme dengan menyalin kromosom dengan nilai fitness tertinggi sebanyak satu atau dua. Siklus ini akan terjadi berulang dan diharapkan pada generasi selanjutnya kromosom yang terbentuk akan memiliki nilai fitness yang semakin baik. Siklus atau proses iterasi akan berhenti ketika tujuan atau persyaratan yang diinginkan terpenuhi [23], [24].

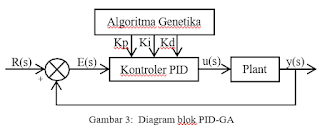
F. Kontroler PID Algoritma Genetika (PID-GA)

Kontroler PID-GA menggunakan metode algoritma genetika dalam mengoptimasi proses tuning parameter PID (Kp, Ki dan Kd). Metode optimasi algoritma genetika bekerja dengan mencari nilai parameter PID terbaik berdasarkan fungsi fitness yaitu meminimalkan error antara nilai setpoint dan nilai aktualnya.. Algoritma bekerja dengan mencari nilai awal parameter secara acak dalam batasan ruang pencarian yang ditetapkan dan berhenti ketika memenuhi kondisi stopping. Paramater terbaik yang diperoleh kemudian akan diterapkan pada kontroler [14]. Kontroler PID-AG diilustrasikan pada gambar 3.

Metodologi Penelitian [Kembali]

A. Blok Diagram Sistem

Kontrol PID berfungsi untuk mengatur nilai input tegangan pada plant motor DC. Penetuan nilai sinyal kontrol yang diberikan bergantung pada selisih nilai error antara kecepatan referensi (setpoint) dengan kecepatan aktualnya. Algortima genetika digunakan untuk mengoptimasi nilai parameter PID yaitu Kp , Ki dan Kd untuk mendapatkan performa terbaik. Blok model matematika motor DC merupakan gambaran sistem berdasarkan persamaan yang telah dijabarkan pada pembahasan tinjauan pustaka. Blok TL merupakan gangguan yang diberikan pada plant berupa torsi beban dengan nilai tertentu. Blok diagram sistem ditunjukkan pada gambar 4.

B. Perancangan Sistem Kontrol pada Simulink

Penelitian ini dilakukan melalui simulasi terhadap plant motor DC terkendali jangkar yang digunakan dalam penilitian sebelumnya [25]. Data spesifikasi mengenai motor DC dirincikan pada tabel 2 berikut.

Dari parameter daya dan kecepatan nominal motor pada tabel 2 di atas, dapat dihitung nilai torsi yang dihasilkan oleh motor DC dengan persamaan berikut [26].

𝑇𝑜𝑟𝑠𝑖 (𝑓𝑡. 𝑙𝑏) = 5252 𝑥 𝑃𝐻𝑃

𝑅𝑎𝑡𝑒𝑑 𝑅𝑃𝑀 (8)

Satuan torsi yang digunakan pada penelitian ini yaitu Nm, maka perlu dikonversi dengan persamaan berikut.

1 𝑓𝑡. 𝑙𝑏 = 1,356 𝑁𝑚 (9)

Model perancangan diagram blok sistem kontrol motor DC pada Simulink dapat diperhatikan pada gambar 5. Sistem diberikan masukan berupa referensi kecepatan sudut sebesar 1500 rpm. Nilai dalam rpm ini dikonversi ke nilai rad/s. Parameter kontrol PID (Kp, Ki dan Kd) diperoleh melalui tuning dengan metode optimasi algoritma genetika. Umpan balik dari sistem berupa kecepatan aktual pada motor DC akan dibandingkan dengan kecepatan referensi untuk menghasilkan sinyal dari pengontrolan PID guna menjaga kecepatan motor sesuai dengan input. Torsi beban dalam beberapa variasi nilai diberikan sebagai gangguan eksternal pada sistem. Blok To Workspace digunakan untuk mengekspor Scope Simulink ke Workspace MATLAB.

Program algoritma genetika sebagai metode tuning kontrol PID pada penelitian ini dijalankan dengan menggunakan script coding pada editor MATLAB dengan diagram alir seperti gambar 6. Tiap kromosom dalam populasi algoritma genetika terdiri atas 3 informasi yaitu nilai Kp, Ki dan Kd. Proses pembentukan populasi awal dalam algoritma genetika dilakukan dengan pencarian secara acak dengan pembatasan ruang pencarian berupa nilai batas. Nilai awal ketiga individu akan diperoleh dengan melakukan tuning secara trial and error digunakan sebagai nilai batas atas. Proses algoritma ini menggunakan dua operator yaitu crossover dan mutasi untuk pembentukan populasi baru pada generasi selanjutnya. Tiap generasi akan dilakukan seleksi berdasarkan nilai fitness untuk mendapatkan solusi terbaik. Program akan berhenti berjalan ketika mencapai jumlah generasi maksimal. Fungsi fitness yang digunakan yaitu Inverse Integral Squared Error dengan persamaan sebagai berikut [16].

Hasil dan Pembahasan[Kembali]

A. Simulasi Kontrol PID pada Sistem

Pada tahap awal percobaan dilakukan proses tuning kontrol PID dengan metode trial and error. Nilai parameter yang diperoleh yaitu Kp = 15; Ki = 30 dan Kd = 1. Performa sistem yang diperoleh dengan parameter ini dapat dilihat pada gambar 7.

Grafik respon sistem yang dihasilkan menunjukkan masih terdapat overshoot sebesar 3,2928 %, sedangkan nilai steady-state error yang dihasilkan sudah kecil sebesar 0,0112%. Nilai rise time sebesar 0,1330 s dan settling time sebesar 0,6996 s.

B. Simulasi Kontrol PID dengan Metode Algortima Genetika

Pada tahap ini dilakukan simulasi dengan menggunakan metode tuning algoritma genetika untuk memperoleh nilai Kp, Ki dan Kd. Nilai yang diperoleh dari metode trial and error digunakan sebagai nilai batas atas dan nilai batas bawah ketiganya sebesar 0,0001. Parameter algortima genetika yang digunakan dapat dilihat pada tabel 3.

Simulasi dilakukan menggunakan enam parameter dengan ukuran populasi, jumlah generasi, probabilitas crossover dan probabilitas mutasi yang bervariasi. Tiap kali algoritma dijalankan pada parameter yang sama kemungkinan dapat memberi hasil yang berbeda. Oleh karenanya tiap parameter diuji cobakan sebanyak lima kali untuk mendapatkan nilai fitness terbaik.

1) Parameter Percobaan 1: Pada parameter percobaan 1, ukuran populasi sebesar 50, jumlah generasi sebesar 50, probabilitas crossover sebesar 0,7 dan probabilitas mutasi sebesar 0,3. Hasil running program ditampilkan dalam bentuk grafik nilai fitness pada gambar 8. Grafik menunjukkan nilai fitness tertinggi yaitu sebesar 4,855e+15. Berdasarkan percobaan menggunakan parameter 1 diperoleh hasil tuning dengan nilai Kp = 8,4605; Ki = 14,1936 dan Kd = 0,19312.

2) Parameter Percobaan 2: Pada parameter percobaan 2, ukuran populasi sebesar 50, jumlah generasi sebesar 50, probabilitas crossover sebesar 0,7 dan probabilitas mutasi sebesar 0,4. Hasil running program ditampilkan dalam bentuk grafik nilai fitness pada gambar 9. Grafik menunjukkan nilai fitness tertinggi yaitu sebesar 8,469e+15. Berdasarkan percobaan menggunakan parameter 2 diperoleh hasil tuning dengan nilai Kp = 1,3491; Ki = 18,1819 dan Kd = 0,2415.

Parameter Percobaan 3: Pada parameter percobaan 3, ukuran populasi sebesar 50, jumlah generasi sebesar 50, probabilitas crossover sebesar 0,8 dan probabilitas mutasi sebesar 0,4. Hasil running program ditampilkan dalam bentuk grafik nilai fitness pada gambar 10. Grafik menunjukkan nilai fitness tertinggi yaitu sebesar 2,399e+16. Berdasarkan percobaan menggunakan parameter 3 diperoleh hasil tuning dengan nilai Kp = 1,6716; Ki = 22,9619 dan Kd = 0,25371.

4) Parameter Percobaan 4: Pada parameter percobaan 4, ukuran populasi sebesar 50, jumlah generasi sebesar 70, probabilitas crossover sebesar 0,9 dan probabilitas mutasi sebesar 0,4. Hasil running program ditampilkan dalam bentuk grafik nilai fitness pada gambar 11. Grafik menunjukkan nilai fitness tertinggi yaitu sebesar 7,787e+17. Berdasarkan percobaan menggunakan parameter 4 diperoleh hasil tuning dengan nilai Kp = 4,6188; Ki = 20,2053 dan Kd = 0,24345.

5) Parameter Percobaan 5: Pada parameter percobaan 5, ukuran populasi sebesar 70, jumlah generasi sebesar 70, probabilitas crossover sebesar 0,9 dan probabilitas mutasi sebesar 0,4. Hasil running program ditampilkan dalam bentuk grafik nilai fitness pada gambar 12. Grafik menunjukkan nilai fitness tertinggi yaitu sebesar 6,261e+18. Berdasarkan percobaan menggunakan parameter 5 diperoleh hasil tuning dengan nilai Kp = 9,4429; Ki = 19,3255 dan Kd = 0,45602.

6) Parameter Percobaan 6: Pada parameter percobaan 6, ukuran populasi sebesar 70, jumlah generasi sebesar 70, probabilitas crossover sebesar 0,9 dan probabilitas mutasi sebesar 0,5. Hasil running program ditampilkan dalam bentuk grafik nilai fitness pada gambar 13. Grafik menunjukkan nilai fitness tertinggi yaitu sebesar 6,341e+17. Berdasarkan percobaan menggunakan parameter 6 diperoleh hasil tuning dengan nilai Kp = 12,8299; Ki = 26,8035 dan Kd = 0,41693.

C. Simulasi Kontrol PID-AG Tanpa Beban

Pada tahap ini dilakukan simulasi pada sistem tanpa beban dengan menggunakan nilai Kp, Ki dan Kd yang diperoleh dari keenam percobaan sebelumnya. Uji coba dilakukan untuk mendapatkan parameter yang memberikan respon sistem terbaik saat sistem dijalankan tanpa mendapatkan beban kerja. Grafik respon sistem yang dihasilkan dari hasil tuning PID dengan keenam parameter percobaan dapat dilihat pada gambar 14.

Data respon sistem dari keenam parameter percobaan dapat dilihat pada tabel 4. Dari parameter percobaan tersebut diperoleh nilai rise time dan settling time terbaik pada parameter percobaan keenam sebesar 0,0816 s dan 0,1783 s berturut-turut. Untuk nilai overshoot terbaik diperoleh pada parameter percobaan kelima sebesar 0,0366 %. Sedangkan untuk nilai steady-state error terbaik diperoleh pada parameter percobaan kedua sebesar 0,0260 %, akan tetapi parameter ini masih menghasilkan overshoot yang tinggi sebesar 15,5668 %. Terdapat 2 parameter terbaik pada percobaan ini yaitu parameter 5 dan parameter 6. Untuk percobaan selanjutnya parameter 5 akan digunakan dengan nilai Kp sebesar 9,4429; Ki sebesar 19,3255 dan Kd sebesar 0,45602. Performa sistem yang diperoleh dengan metode algoritma genetika ini kemudian dibandingkan dengan metode trial and error seperti pada tabel 5.

TABEL 5 PERBANDINGAN PERFORMA SISTEM

Metode

Tuning

Rise time (s)

Settling time (s)

Oversho ot (%)

Steady- state

error (%)

Algoritma

genetika

0,1212

0,2562

0,0366

0,1739

Trial and error

0,1330

0,6996

3,2928

0,0112

Pada tabel 5 dapat dilihat bahwa hasil tuning dengan metode algoritma genetika dapat memberikan nilai rise time, settling time, dan overshoot yang lebih baik dari metode trial and error. Akan tetapi nilai steady-state error yang dihasilkan dengan metode algoritma genetika masih lebih besar dibandingkan dengan metode trial and error. Secara keseluruhan performa sistem yang dihasilkan dengan metode algoritma genetika mampu memberikan respon sistem yang lebih optimal.

D. Simulasi Kontrol PID-AG dengan Beban

Pada tahap ini dilakukan simulasi dengan memberikan gangguan berupa beban tetap dan beban yang berubah. Parameter kontroler PID yang digunakan yaitu Kp = 9,4429; Ki = 19,3255 dan Kd = 0,45602. Untuk menghitung beban nominal yang diberikan dapat dihitung dengan mengacu pada (8) dan (9) dan datasheet motor DC pada tabel 2.

T𝑜𝑟𝑠𝑖 = 5252 𝑥 2 1500 = 7,0027 𝑓𝑡. 𝑙𝑏 = 7,0027 𝑥 1.356 = 9,49 𝑁𝑚 = 9,5 𝑁

1) Pemberian Beban Tetap: Percobaan pertama dilakukan dengan memberikan beban kerja bernilai tetap pada sistem sebesar 9,5 Nm pada saat t = 2 s. Respon sistem dapat dilihat pada gambar 15. Grafik menunjukkan ketika beban diberikan terjadi penurunan kecepatan hingga 1485 rpm, berkurang 15 rpm. Kecepatan motor kembali ke nilai setpoint pada saat t = 3,6 s yang berarti dibutuhkan waktu kurang dari 2 s untuk mencapai kondisi stabil ketika motor diberi beban kerja.

Percobaan kedua dilakukan dengan memberikan gangguan berupa beban tetap pada sistem sebesar 14 Nm pada saat t = 2s. Respon sistem dapat dilihat pada gambar 16. Grafik menunjukkan bahwa ketika beban diberikan sebesar 14 Nm terjadi penurunan kecepatan hingga 1478 rpm. Kecepatan motor kembali ke nilai setpoint pada saat t = 3,8 s, meskipun masih terdapat fluktuasi sebesar 1 rpm. Nilai kecepatan stabil ketika t = 5,8 s, sehingga dibutuhkan waktu kurang dari 6 detik untuk sistem dapat kembali berjalan mengikuti nilai setpoint.

Percobaan ketiga dilakukan dengan memberikan gangguan berupa beban tetap pada sistem sebesar 16.5 Nm pada saat t = 2 s. Respon sistem dapat dilihat pada gambar 17. Grafik menunjukkan bahwa ketika beban diberikan sebesar 16,5 Nm terjadi penurunan kecepatan hingga 1474 rpm,. Kecepatan motor kembali ke nilai setpoint pada saat t = 4 s yang berarti membutuhkan waktu 2 detik. Akan tetapi kecepatan masih mengalami fluktuasi sebesar 1 rpm. Nilai kecepatan stabil ketika t = 6 s, sehingga dibutuhkan waktu 4 detik untuk sistem dapat kembali berjalan mengikuti nilai setpoint meski diberikan beban di atas nilai nominalnya.

2) Pemberian Beban Tidak Tetap: Pada pengujian ini sistem dijalankan dengan diberi nilai torsi beban yang bervariasi. Pada saat t = 0 s beban diberikan sebesar 9,5 Nm, lalu pada saat t = 3 s beban dinaikkan menjadi 15 Nm, kemudian saat t = 6 s beban kembali diturunkan pada nilai 9,5 Nm. Respon sistem dapat dilihat pada gambar 18. Pada percobaan motor DC diberikan beban sebesar 9,5 Nm dari awal dijalankan. Sehingga dibutuhkan waktu lebih lama untuk mencapai nilai setpoint yaitu 2,4 s. Ketika beban dinaikkan menjadi 15 Nm kecepatan turun menjadi 1491 rpm. Kemudian saat beban diturunkan lagi menjadi 9,5 Nm kecepatan naik hingga 1509 rpm dan dibutuhkan kurang dari 1,5 detik untuk kembali stabil di nilai setpoint. Melalui percobaan ini maka diketahui bahwa sistem mampu mempertahankan nilai kecepatan pada setpoint meskipun dalam keadaan nilai beban yang berubah.

Kesimpulan[Kembali]

Berdasarkan hasil percobaan yang dilakukan diperoleh solusi dengan nilai fitness tertinggi sebesar 6,261e+18 dengan parameter ukuran populasi dan jumlah generasi sebesar 70, probabilitas crossover sebesar 0,9 dan probabilitas mutasi sebesar 0,4. Parameter PID terbaik diperoleh dengan nilai Kp = 9,4429; Ki = 19,3255 dan Kd = 0,45602. Respon sistem yang dihasilkan dengan parameter ini memiliki nilai rise time sebesar 0,1212 s, settling time sebesar 0,2562 s, overshoot sebesar 0,0366 % dan steady-state error sebesar 0,1739 %. Kontrol PID dengan tuning menggunakan metode algoritma genetika terbukti mampu menjaga kecepatan motor pada nilai setpoint ketika diberi beban kerja baik dengan nilai tetap maupun nilai yang berubah. Untuk pengembangan ke depannya diharapkan tuning PID dengan metode algoritma genetika dapat diterapkan dalam berbagai sistem pengontrolan lainnya. Selain itu pengkajian mendalam mengenai algoritma genetika dapat dilakukan terutama mengenai fungsi fitness guna menghasilkan respon sistem yang lebih optimal.

Daftar Pustaka[Kembali]

[1] A. Ma’rifat, N. R. Setiawan, and E. S. Rahayu, “Embedded Control System of DC Motor Using Microcontroller Arduino and PID Algorithm,” IT Journal Research and Development, vol. 6, no. 1, pp. 30–42, 2021, doi: 10.25299/itjrd.2021.vol6(1).6125.

[2] D. A. Barkas, G. C. Ioannidis, C. S. Psomopoulos, S. D. Kaminaris, and G. A. Vokas, “Brushed DC Motor Drives for Industrial and Automobile Applications with Emphasis on Control Techniques: A Comprehensive Review,” Electronics, vol. 9, p. 887, 2020, doi: 10.3390/electronics9060887.

[3] A. MA’ARIF, R. ISTIARNO, and SUNARDI, “Kontrol Proporsional Integral Derivatif (PID) pada Kecepatan Sudut Motor DC dengan Pemodelan Identifikasi Sistem dan Tuning,” ELKOMIKA Jurnal Teknik Energi Elektrik, Teknik Telekomunikasi, vol. 9, no. 2, pp. 374–388, 2021, doi: 10.26760/elkomika.v9i2.374.

[4] A. Budiyanto and A. Intan Ekaputri Supriyo, “PERBANDINGAN METODE PID, MPC, DAN LQR PADA SISTEM PEMANAS AIR BOTTLE WASHER BERBASIS MATLAB,” AJIE - Asian Journal of Innovation and Entrepreneurship, vol. 05, no. 03, pp. 35–43, 2020.

[5] Z. Peng, “PID Control of Temperature and Humidity in Granary Based on Improved Genetic Algorithm,” in 2019 IEEE International Conference on Power, Intelligent Computing and Systems (ICPICS), 2019, pp. 428–432.

[6] S. K. Pandey, C. Bera, and S. S. Dwivedi, “Design of robust PID controller for DC Motor using TLBO algorithm,” in 2020 IEEE International Conference on Advances and Developments in Electrical and Electronics Engineering (ICADEE), 2020, pp. 1–4. doi: 10.1109/ICADEE51157.2020.9368952.

[7] M. Irhas, Iftitah, and S. Asyiqah Azizah Ilham, “Penggunaan Kontrol PID dengan Berbagai Metode untuk Analisis Pengaturan Kecepatan Motor DC,” Jurnal Fisika dan Terapannya, vol. 7, no. 1, pp. 78–86, 2020.

[8] A. Ma’rifat, H. Nabila, and O. Wahyunggoro, “Application of Intelligent Search Algorithms in Proportional-Integral- Derivative Control of Direct-Current Motor System Application of Intelligent Search Algorithms in Proportional- Integral-Derivative Control of Direct-Current Motor System,” in Journal of Physics: Conference Series, 2019, vol. 1373, pp. 1–10. doi: 10.1088/1742- 6596/1373/1/012039.

[9] M. Ünal, A. Ak, V. Topuz, and H. Erdal, Optimization of PID Controllers Using Ant Colony and Genetic Algorithms. Springer International Publishing: Berlin/Heidelberg, Germany, 2013. doi: 10.1007/978-3-642-32900-5.

[10] Y. Arkeman, K. B. Seminar, and H. Gunawan, “Algoritma Genetika,” in ALGORTIMA GENETIKA Teori dan Aplikasinya untuk Bisnis dan Industri, Bogor: PT Penerbit IPB Press, 2012, pp. 13–30.

[11] S. Tiwari, A. Bhatt, A. C. Unni, J. G. Singh, and W. Ongsakul, “Control of DC Motor Using Genetic Algorithm Based PID Controller,” Proceedings of the Conference on the Industrial and Commercial Use of Energy, no. October, 2018, doi: 10.23919/ICUE- GESD.2018.8635662.

[12] Z. Abidin and E. Ihsanto, “Perancangan Kontroler PID Level Deaerator Dan Kondensor Pada Steam Power Plant Berbasis Algoritma Genetika,” Jurnal Teknologi Elektro, vol. 12, no. 3, pp. 153–159, 2021, doi: 10.22441/jte.2021.v12i3.009.

[13] E. L. Talakua, Y. A. K. Utama, and I. Andriyanto, “Optimasi Kontrol PID untuk Kendali Kecepatan Motor DC Menggunakan Metode Metaheuristik,” Seminar Nasional Ilmu Terapan, pp. 1–8, 2020.

[14] A. A. M. Zahir, S. S. N. Alhady, W. A. F. W. Othman, and M. F. Ahmad, “Genetic Algorithm Optimization of PID Controller for Brushed DC Motor,” in Intelligent Manufacturing & Mechatronics, Lecture Notes in Mechanical Engineering, Springer Nature Singapore, 2018, pp. 427–437. doi: 10.1007/978-981-10-8788-2_38.

[1] [15] E. W. Suseno and A. Ma’rifat, “Tuning of PID Controller Parameters with Genetic Algorithm Method on DC Motor,” International Journal of Robotics and Control Systems, vol. 1, no. 1, pp. 41–53, 2021, doi: 10.31763/ijrcs.v1i1.249.

[2] [16] J. Beneoluchi, A. Noraziah, and A. Eunice, “A new fitness function for tuning parameters of Peripheral Integral Derivative Controllers,” ICT Express, no. xxxx, pp. 1–5, 2021, doi: 10.1016/j.icte.2021.10.006.

[3] [17] H. Sutrisno, Suryono, and P. H. Hastungkoro, Mengenal Motor Listrik Arus Searah, 1st ed. Klaten: Saka Mitra Kompetensi, 2019.

[4] [18] B. Siswojo, ELEKTRONIKA KONTROL, 1st ed. Malang: UB Press, 2017.

[5] [19] Fahmizal, F. Fathuddin, and R. Susanto, “Identifikasi Sistem Motor DC dan Kendali Linear Quadratic Regulator Berbasis Arduino- Simulink Matlab,” Majalah Ilmiah Teknologi Elektro, vol. 17, no. 2, 2018.

[6] [20] A. H. Rahardjo and W. B. Mursanto, Bahan Ajar Sistem Kendali. POLITEKNIK NEGERI BANDUNG, 2020.

[7] [21] C. P. R. Tuuk, V. C. Poekoel, and J. Litouw, “Implementasi Pengendali PID Untuk Kestabilan Posisi Terbang Wahana Tanpa Awak,” J. Tek. Elektro dan Komput., vol. 7, no. 1, pp. 53–62, 2018.

[8] [22] G. A. Salamena and V. Salamena, “Analisis Penentuan Konstanta Pengendali PID Menggunakan Garis Singgung Metode Ziegler- Nichols I pada Titik Koordinat Kurva Tanggapan Keluaran Plant,” JURNAL SIMETRIK, vol. 10, no. 2, pp. 333–343, 2020.

[9] [23] Z. Zukhri, ALGORITMA GENETIKA Metode Komputasi Evolusioner untuk Menyelesaikan Masalah Optimasi, 1st ed. Yogyakarta: ANDI, 2014.

[10] [24] T. H. Fratiwi, M. Sudarma, and N. Pramaita, “Sistem Klasifikasi Musik Gamelan Angklung Bali Terhadap Suasana Hati Menggunakan Algoritma K-Nearest Neighbor Berbasis Algoritma Genetika,” Majalah Ilmiah Teknologi Elektro, vol. 20, no. 2, pp. 265–272, 2021.

[11] [25] B. Y. Suprapto, A. Azmi, F. Nora, and S. Dwijayanti, “Penalaan Parameter Pengendali PID untuk Pengendalian Kecepatan Motor Arus Searah Menggunakan Metode Algoritma Genetika dan Jaringan Syaraf Tiruan,” Jurnal Riset Sains dan Teknologi, vol. 4, no. 1, pp. 15–23, 2020, doi: 10.30595/ jrst.v4i1.5050.

[12] [26] “Motor Torque Calculator, Full Load Torque of a Motor.” http://www.electricalclassroom.com/full-load-motor (accessed Jan. 24, 2022).

Metode Ziegler-Nichols[Kembali]

Metode Ziegler-Nichols

Ziegler-Nichols pertama kali memperkenalkan metodenya pada tahun 1942. Metode ini memiliki dua cara, metode osilasi dan kurva reaksi. Kedua metode ditujukan untuk menghasilkan respon sistem dengan lonjakan maksimum sebesar 25%. Gambar 11 memperlihatkan kurva dengan lonjakan 25%.

Gambar 11 Kurva respons tangga satuan yang memperlihatkan 25 % lonjakan maksimum

Metode Kurva Reaksi

Metode ini didasarkan terhadap reaksi sistem untaian terbuka. Plant sebagai untaian terbuka dikenai sinyal fungsi tangga satuan (gambar 12). Kalau plant minimal tidak mengandung unsur integrator ataupun pole-pole kompleks, reaksi sistem akan berbentuk S. Gambar 13 menunjukkan kurva berbentuk S tersebut. Kelemahan metode ini terletak pada ketidakmampuannya untuk plant integrator maupun plantt yang memiliki pole kompleks.

Gambar 12 Respon tangga satuan sistem

Gambar 13 Kurva Respons berbentuk S.

Kurva berbentuk-s mempunyai dua konstanta, waktu mati (dead time) L dan waktu tunda T. Dari gambar 13 terlihat bahwa kurva reaksi berubah naik, setelah selang waktu L. Sedangkan waktu tunda menggambarkan perubahan kurva setelah mencapai 66% dari keadaan mantapnya. Pada kurva dibuat suatu garis yang bersinggungan dengan garis kurva. Garis singgung itu akan memotong dengan sumbu absis dan garis maksimum. Perpotongan garis singgung dengan sumbu absis merupakan ukuran waktu mati, dan perpotongan dengan garis maksimum merupakan waktu tunda yang diukur dari titik waktu L.

Penalaan parameter PID didasarkan perolehan kedua konstanta itu. Zeigler dan Nichols melakukan eksperimen dan menyarankan parameter penyetelan nilai Kp, Ti, dan Td dengan didasarkan pada kedua parameter tersebut. Tabel 1 merupakan rumusan penalaan parameter PID berdasarkan cara kurva reaksi.

Tabel 1 Penalaan paramater PID dengan metode kurva reaksi

Tipe Kontroler	K_p	T_i	T_d
P	T/L	~	0
PI	0,9 T/L	L/0.3	0
PID	1,2 T/L	2L	0,5L

Metode Osilasi

Metode ini didasarkan pada reaksi sistem untaian tertutup. Plant disusun serial dengan kontroller PID. Semula parameter parameter integrator disetel tak berhingga dan parameter diferensial disetel nol (T_i = ~ ;T_d = 0). Parameter proporsional kemudian dinaikkan bertahap. Mulai dari nol sampai mencapai harga yang mengakibatkan reaksi sistem berosilasi. Reaksi sistem harus berosilasi dengan magnitud tetap(Sustain oscillation) (Guterus, 1994, 9-9). Gambar 14 menunjukkan rangkaian untaian tertutup pada cara osilasi.

Gambar 14 Sistem untaian tertutup dengan alat kontrol proporsional

Nilai penguatan proportional pada saat sistem mencapai kondisi sustain oscillation disebut ultimate gain K_u. Periode dari sustained oscillation disebut ultimate period T_u (Perdikaris, 1991, 433). Gambar 15 menggambarkan kurva reaksi untaian terttutup ketika berosilasi.

Gambar 15 Kurva respon sustain oscillation

Penalaan parameter PID didasarkan terhadap kedua konstanta hasil eksperimen, Ku dan Pu. Ziegler dan Nichols menyarankan penyetelan nilai parameter K_p, T_i, dan T_dberdasarkan rumus yang diperlihatkan pada Tabel 2.

Tabel 2 Penalaan paramater PID dengan metode osilasi

Tipe Kontroler	K_p	Ti	Td
P	0,5.K_u
PI	0,45.K_u	1/2 P_u
PID	0,6.K_u	0,5 P_u	0,125 P_u

Metode Quarter - decay

Karena tidak semua proses dapat mentolerir keadaan osilasi dengan amplituda tetap, Cohen-coon berupaya memperbaiki metode osilasi dengan menggunakan metode quarter amplitude decay. Tanggapan untaian tertutup sistem, pada metode ini, dibuat sehingga respon berbentuk quarter amplitude decay (Guterus, 1994, 9-13). Quarter amplitude decay didefinisikan sebagai respon transien yang amplitudanya dalam periode pertama memiliki perbandingan sebesar seperempat (1/4) (Perdikaris, 1991, 434).

Gambar 16 Kurva respon quarter amplitude decay

Kontroler proportional K_p ditala hingga diperoleh tanggapan quarter amplitude decay, periode pada saat tanggapan ini disebut T_p dan parameter T_i dan T_d dihitung dari hubungan (Perdikaris, 434, 1990). Sedangkan penalaan parameter kontroler PID adalah sama dengan yang digunakan pada metode Ziegler-Nichols (lihat tabel 1 - untuk metode kurva reaksi dan tabel 2 untuk metode osilasi).

Mencari nilai Kp, Ki, dan Kd Menggunakan Metode Ziegler-Nichols I[Kembali]